Python-MNE 脑电脑磁分析指南
这是一个结合了个人经验和官网翻译的个人MNE学习笔记
开始使用

目的

以牺牲深度为代价进行入门学习，简易学习基本方法

开始

导入相关库：

1
2
3
4
# License: BSD-3-Clause
# Copyright the MNE-Python contributors.
import numpy as np
import mne

加载数据

MNE-Python数据结构式基于fif格式的，但是对于其他格式也有阅读方法，如https://mne.tools/stable/documentation/implementation.html#data-formats的Supported data formats部分所示。MNE提供了一个示例数据集，可供学习之用。

现在下载示例数据集开始学习，在以下代码中，导入了一个已经经过滤波的raw示例：

1
2
3
4
5
sample_data_folder = mne.datasets.sample.data_path()
sample_data_raw_file = (
    sample_data_folder / "MEG" / "sample" / "sample_audvis_filt-0-40_raw.fif"
)
raw = mne.io.read_raw_fif(sample_data_raw_file)

Opening raw data file /home/circleci/mne_data/MNE-sample-data/MEG/sample/sample_audvis_filt-0-40_raw.fif…
Read a total of 4 projection items:
PCA-v1 (1 x 102) idle
PCA-v2 (1 x 102) idle
PCA-v3 (1 x 102) idle
Average EEG reference (1 x 60) idle
Range : 6450 … 48149 = 42.956 … 320.665 secs
Ready.

输出是这样的，返回了一个储存示例数据的位置，然后给出了读取数据的具体成分信息和时间长度。

这里它告诉我们，在文件中有四个“projection item（投影项）”和记录的数据；这些是SSP projectors，用于去除MEG信号中的环境噪声，还有一个用于对EEG通道进行均值参考。这些将后面讨论。

除了加载过程中显示的信息外，你还可以通过打印Raw对象来了解它的基本细节。通过打印它的info属性（一个在Raw、epoch和Evoked对象中保留的字典类对象）可以获得更多信息。info中包含channel locations, applied filters, projectors等内容。

1
2
print(raw)
print(raw.info)

<Raw | sample_audvis_filt-0-40_raw.fif, 376 x 41700 (277.7 s), ~3.3 MB, data not loaded>
<Info | 14 non-empty values
bads: 2 items (MEG 2443, EEG 053)
ch_names: MEG 0113, MEG 0112, MEG 0111, MEG 0122, MEG 0123, MEG 0121, MEG …
chs: 204 Gradiometers, 102 Magnetometers, 9 Stimulus, 60 EEG, 1 EOG
custom_ref_applied: False
dev_head_t: MEG device -> head transform
dig: 146 items (3 Cardinal, 4 HPI, 61 EEG, 78 Extra)
highpass: 0.1 Hz
hpi_meas: 1 item (list)
hpi_results: 1 item (list)
lowpass: 40.0 Hz
meas_date: 2002-12-03 19:01:10 UTC
meas_id: 4 items (dict)
nchan: 376
projs: PCA-v1: off, PCA-v2: off, PCA-v3: off, Average EEG reference: off
sfreq: 150.2 Hz

raw对象有几个内置的绘图方法。如下是使用compute_psd显示每个传感器类型的功率谱密度(PSD)。在交互式Python session中，图是允许稍微自由编辑的。

1
2
raw.compute_psd(fmax=50).plot(picks="data", exclude="bads", amplitude=False)
raw.plot(duration=5, n_channels=30)

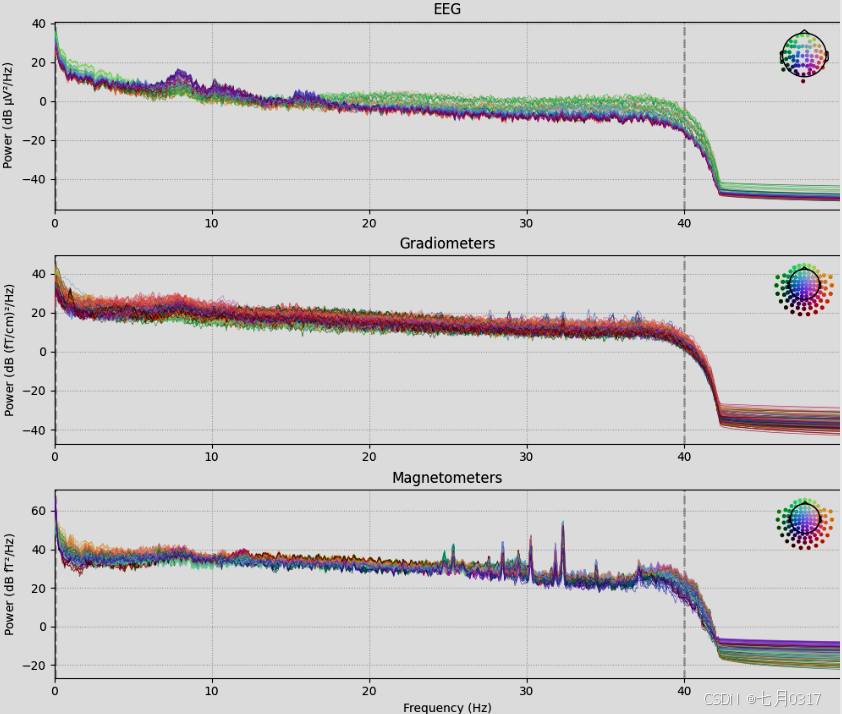
image.png

image.png
当然，如果要用jupyter等写代码，请魔术命令%matplotlib一下方便绘图。

预处理

MNE-Python支持多种预处理方法和技术，如maxwell滤波、信号空间投影、独立分量分析、滤波、降采样等。在这里，我们将通过ICA分析来clean up我们的数据（简单版）。

ICA即独立成分分析。它的基本思想是将复杂的观测数据分解成多个独立的成分，每个成分都代表数据中的一个源或者生成过程。

ICA 的工作原理类似于解开信号混叠的拼图。假设我们有多个不同的信号源同时混合在一起，通过 ICA，我们可以将混合后的信号分解为多个相互独立的成分。这些成分在统计上是相互独立的，并且每个成分都包含了数据中某个特定的信号源的信息。因此，ICA 可以帮助我们从复杂的观测数据中提取出有用的信息，比如识别出不同脑区域的活动或者分离出不同的生理信号。

1
2
3
4
5
6
7
8
9
# set up and fit the ICA
# 这里就ICA了20个成分，这只是生成一个ICA算子
ica = mne.preprocessing.ICA(n_components=20, random_state=97, max_iter=800)
# 然后应用在raw上
ica.fit(raw)
# 排除1号和2号
ica.exclude = [1, 2]  # details on how we picked these are omitted here
# 展示一下排除的东西，可以看到1是心电伪迹，2是眼动伪迹，具体不详细展开
ica.plot_properties(raw, picks=ica.exclude)

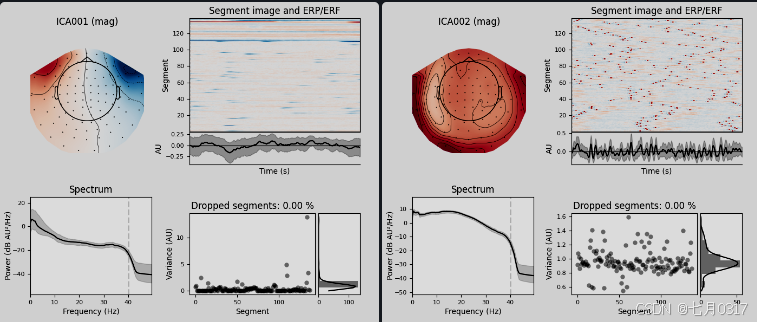
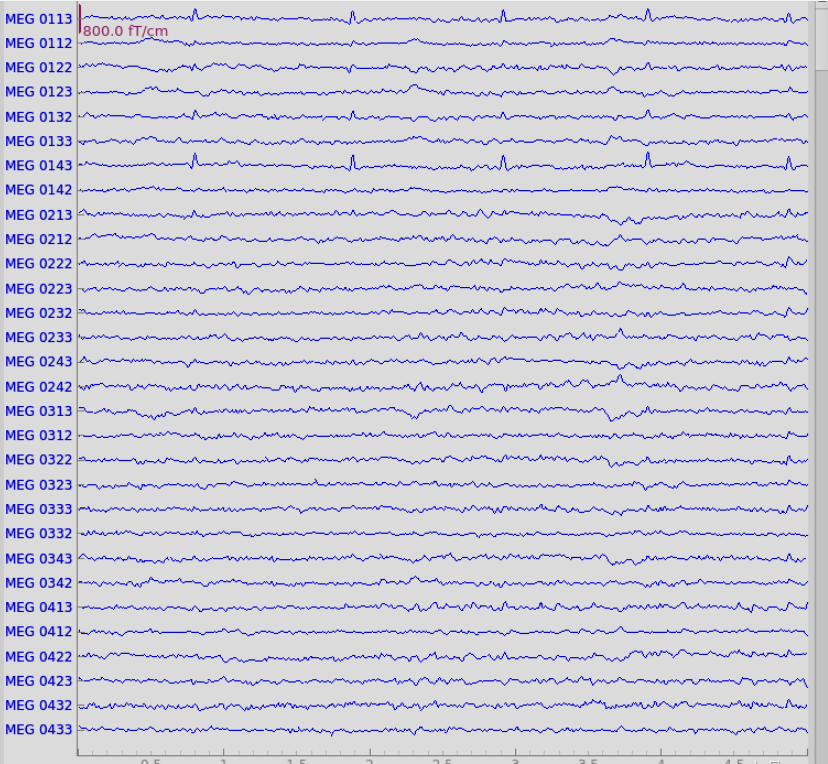
image.png
一旦确认了坏的ica成分，我们就惊醒应用，注意这里是in place的操作，所以先copy一个备份。apply方法要求将raw数据加载到内存中（默认情况下是不加载的），因此我们将首先使用load_data。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
orig_raw = raw.copy()
raw.load_data()
ica.apply(raw)

# show some frontal channels to clearly illustrate the artifact removal
chs = [
    "MEG 0111",
    "MEG 0121",
    "MEG 0131",
    "MEG 0211",
    "MEG 0221",
    "MEG 0231",
    "MEG 0311",
    "MEG 0321",
    "MEG 0331",
    "MEG 1511",
    "MEG 1521",
    "MEG 1531",
    "EEG 001",
    "EEG 002",
    "EEG 003",
    "EEG 004",
    "EEG 005",
    "EEG 006",
    "EEG 007",
    "EEG 008",
]
chan_idxs = [raw.ch_names.index(ch) for ch in chs]
orig_raw.plot(order=chan_idxs, start=12, duration=4)
raw.plot(order=chan_idxs, start=12, duration=4)

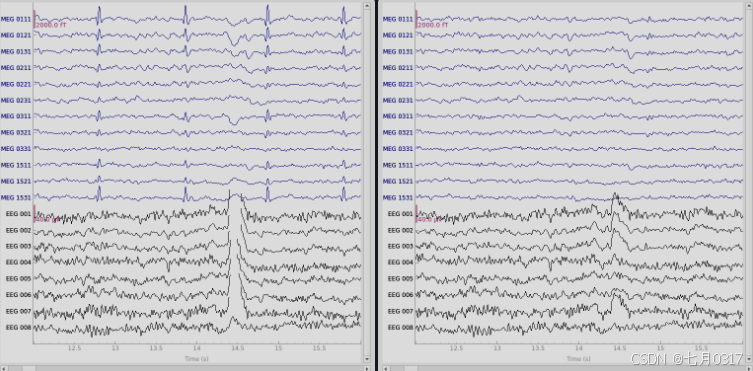
image.png
以上展示了一些EEG通道，orig_raw.plot和raw.plot对比，可以看到额部的眼电和心电伪迹被去除了。

探测事件

你在程序里放的trigger，记录在STIM通道上，现在给它读取一下。

1
2
events = mne.find_events(raw, stim_channel="STI 014")
print(events[:5])  # show the first 5

319 events found on stim channel STI 014
Event IDs: [ 1 2 3 4 5 32]
[[6994 0 2]
[7086 0 3]
[7192 0 1]
[7304 0 4]
[7413 0 2]]

这个结果是一个numpy array，所以要用numpy array的方法处理，这里不详述。第一列是时间，是开始时间+采样率*秒，第二列可以忽略，第三列是你设计的值，有的时候自动探测会出错，要人工修改。

现在设置一个event字典命名这几个trigger值。

1
2
3
4
5
6
7
8
event_dict = {
    "auditory/left": 1,
    "auditory/right": 2,
    "visual/left": 3,
    "visual/right": 4,
    "smiley": 5,
    "buttonpress": 32,
}

注意，这里字典键中的“/”可以提供请求“auditory”然后返回event id为1和2的所有event的方法。

然后我们画出来看看：

1
2
3
fig = mne.viz.plot_events(
    events, event_id=event_dict, sfreq=raw.info["sfreq"], first_samp=raw.first_samp
)

注意这里的采样率和开始节点参数。

然后设置一个拒绝字典，高于这个值的就不要。

1
2
3
4
5
6
reject_criteria = dict(
    mag=4000e-15,  # 4000 fT
    grad=4000e-13,  # 4000 fT/cm
    eeg=150e-6,  # 150 µV
    eog=250e-6,
)  # 250 µV

epoch可以理解为每个event事件前后一小段时间的数据，是分析的基本单位，现在我们创建epoch对象，应用我们的拒绝字典。

1
2
3
4
5
6
7
8
9
epochs = mne.Epochs(
    raw,
    events,
    event_id=event_dict,
    tmin=-0.2,
    tmax=0.5,
    reject=reject_criteria,
    preload=True,
)

Not setting metadata
319 matching events found
Setting baseline interval to [-0.19979521315838786, 0.0] s
Applying baseline correction (mode: mean)
Created an SSP operator (subspace dimension = 4)
4 projection items activated
Using data from preloaded Raw for 319 events and 106 original time points …
Rejecting epoch based on EOG : [‘EOG 061’]
Rejecting epoch based on EOG : [‘EOG 061’]
Rejecting epoch based on MAG : [‘MEG 1711’]
Rejecting epoch based on EOG : [‘EOG 061’]
Rejecting epoch based on EOG : [‘EOG 061’]
Rejecting epoch based on MAG : [‘MEG 1711’]
Rejecting epoch based on EEG : [‘EEG 008’]
Rejecting epoch based on EOG : [‘EOG 061’]
Rejecting epoch based on EOG : [‘EOG 061’]
Rejecting epoch based on EOG : [‘EOG 061’]
10 bad epochs dropped

可以看到有10个bad epochs被拒绝了。

然后我们汇聚左右两种刺激，以比较总体的听觉和视觉反应。为了避免信号向左或者向右的偏倚，我们首先用equalize_event_counts的方法去从每种条件（左或右）中随机抽样epoch，以匹配二者的数量，因为之前不是拒绝掉了一些嘛。

注意注释，有的步骤是in-place的。这里就应用到了之前我们说的“/”字典键的用处。

1
2
3
4
5
conds_we_care_about = ["auditory/left", "auditory/right", "visual/left", "visual/right"]
epochs.equalize_event_counts(conds_we_care_about)  # this operates in-place
aud_epochs = epochs["auditory"]
vis_epochs = epochs["visual"]
del raw, epochs  # free up memory

Dropped 7 epochs: 121, 195, 258, 271, 273, 274, 275

然后对epoch进行火兔，展示某个通道的epoch的功率图，这里展示了一个颞部和顶部的电极的对比。

1
aud_epochs.plot_image(picks=["MEG 1332", "EEG 021"])

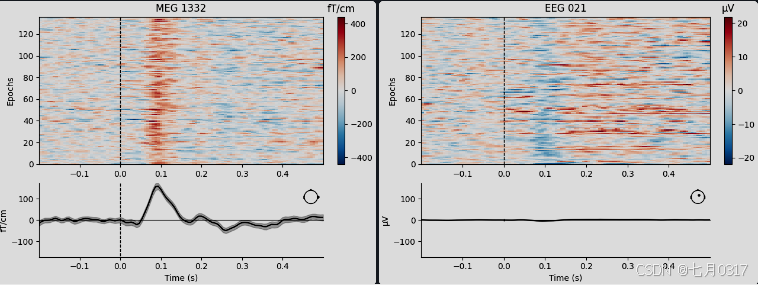
image.png

注意，raw和epoch对象都有get_data方法，这些方法将底层数据作为numpy array返回。这两个方法都有一个picks参数，用于选择要返回的通道。

raw.get_data()具有用于限制时间的附加参数。生成的矩阵对raw对象具有维度(n_channels, n_times)，对epochs对象具有维度(n_epochs, n_channels, n_times)。

时频分析

mne的Time_frequency子模块提供了几种算法来进行视频分析、功率谱密度和交叉谱密度。在这里，我们将计算听觉epoch在不同频率和时间的感应功率，使用Morlet wavelet的方法。在这个数据集上，结果只是显示了诱发的听觉N100反应。

1
2
3
4
5
frequencies = np.arange(7, 30, 3)
power = aud_epochs.compute_tfr(
    "morlet", n_cycles=2, return_itc=False, freqs=frequencies, decim=3, average=True
)
power.plot(["MEG 1332"])

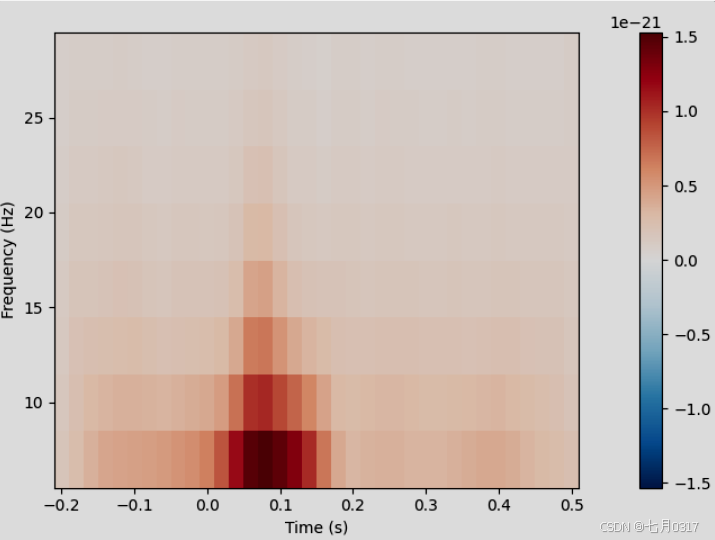
image.png

估计evoked反应

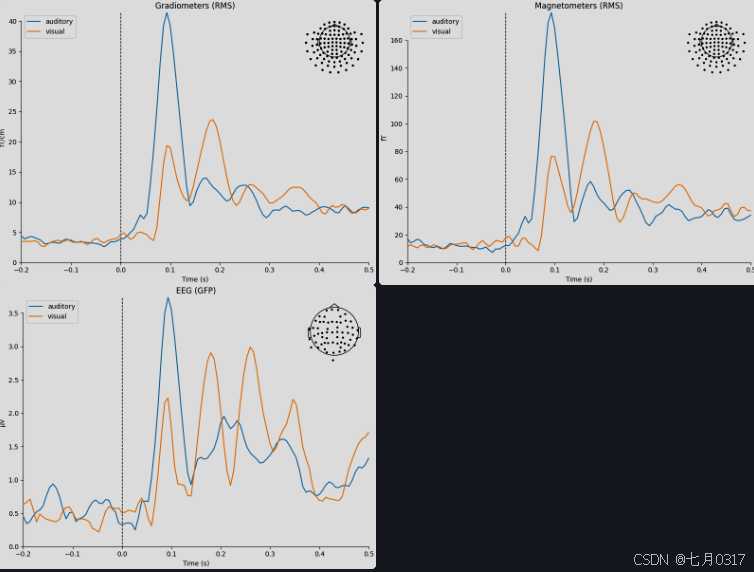
现在我们有了aud_epochs和vis_epochs，我们可以通过平均每种条件（听觉或视觉）下的所有epoch来估计听觉和视觉刺激的诱发反应，这就是evoked。这非常简单，只需调用Epochs对象上的average方法，然后使用mne.viz模块来比较两个evoked对象的每个传感器类型的全局场强:

1
2
3
4
5
6
7
8
aud_evoked = aud_epochs.average()
vis_evoked = vis_epochs.average()

mne.viz.plot_compare_evokeds(
    dict(auditory=aud_evoked, visual=vis_evoked),
    legend="upper left",
    show_sensors="upper right",
)

image.png
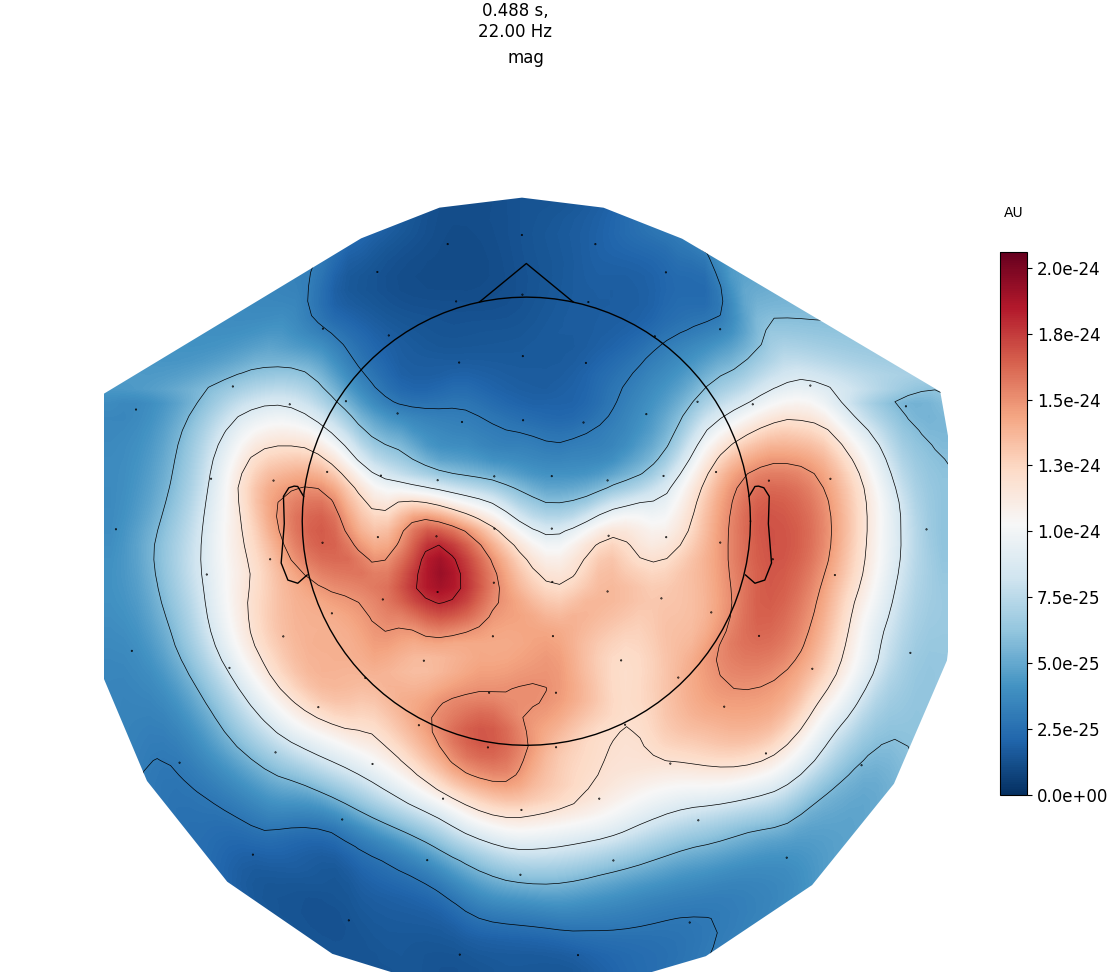
我们还可以得到关于evoked的具体细节，得到一个topomap，如下所示：

1
2
aud_evoked.plot_joint(picks="eeg")
aud_evoked.plot_topomap(times=[0.0, 0.08, 0.1, 0.12, 0.2], ch_type="eeg")

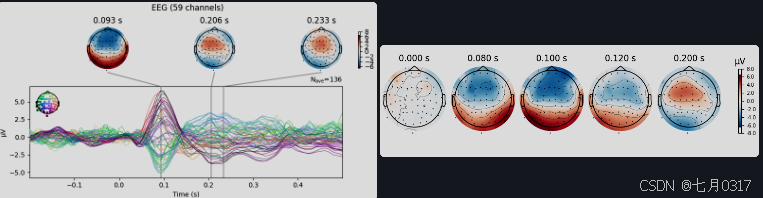
image.png
evoked对象还可以被合并，然后一起比较全脑的相应差异，传递一个weights=[1, -1]即可（听觉是1，视觉是-1）.

1
2
evoked_diff = mne.combine_evoked([aud_evoked, vis_evoked], weights=[1, -1])
evoked_diff.pick(picks="mag").plot_topo(color="r", legend=False)

image.png

逆运算

这里简单演示了源定位。
以下是源定位相关知识，来自百度和gpt老师：

一般认为，脑电图(EEG)的主要产生器是发生在锥体皮层神经元上的突触后电位。这些突触电流的同步活动导致了脑内的电流流动。
由于头部是导电介质，容积传导允许这些电流传播到头皮表面，在那里它们会在放置在头皮不同位置的电极之间产生电位差。通过使用电极阵列记录这些电位，可以构建地形图，显示活跃神经元群在任何给定时刻产生的头皮电位分布。如果只有一个脑区活动，则头皮上的电位分布相当简单和偶极。然而，如果大脑的几个区域同时活跃，就会出现头皮电位的复杂模式，而推断潜在的来源就成为一项艰巨的任务。一般来说，需要进行先验假设，优先结合解剖学、生理学和生物物理学知识。
一个重要的发展是引入头部的解剖约束，以促进解决EEG源定位问题。进一步的发展引入了皮层源的生理约束，以促进解决分布式源成像问题。尽管只是对潜在源的估计，但是这种先验约束极大地提高了EEG源定位的可解性和精确性。

EEG源定位的第一次尝试是基于强大的先验假设，即在某个时间点只有一个源是活跃的，头部可以近似为一个球体，并且整个大脑的电导率是均匀的。在这种情况下，非线性多维优化方法允许在大脑中发现等效偶极子的位置、方向和强度，以最好地解释所观察到的头皮电位测量。很快，不同组织之间的电导率差异被纳入多层球形头部模型中，最终，基于磁共振(MR)图像的真实几何头部模型被开发出来，使用边界或有限元重建头皮和不同组织。逆模型从一个或几个时变偶极子的强约束发展到估计整个脑容量中三维电流密度分布的分布式源重建方法。
MEG也是一样的。
MEG正问题：
由同步突触后电位产生的电势在大脑中不均匀地传播。不同的组织，如头皮、颅骨、脑脊液和大脑，具有不同的导电特性，因此会在不同程度上衰减电流。如果电导率参数已知并正确选择，泊松方程允许在每个头皮电极上确定由大脑中已知源产生的电势。因此，源通常被建模为等效电流偶极子，由一对源电流和汇电流组成，代表流经皮层锥体细胞顶端树突状的突触后电流。由这种源产生的头皮电位的计算通常被称为正问题。
目前解决EEG正问题的方法是边界元法(BEM)。BEM的使用允许将头部的解剖信息，以及主要的电导率特征(如大脑、颅骨和头皮)合并到EEG正向解中。BEM用三角形网格对头部每个组织之间的接口进行建模，例如空气/头皮、头皮/颅骨和颅骨/大脑接口。每种类型的组织被认为是电均质的和各向同性的，并给出了每种组织不同的电导率值。另一方面，有限元方法(FEM)已被用于模拟白质内的组织电导率不均匀性和电导率各向异性分布。这
些数值技术利用MRI提供的解剖信息来分割不同的脑组织和头部结构。
MEG逆问题：
确定在头皮上产生给定EEG(或MEG)测量的颅内源是电磁逆问题的挑战。包括偶极子源定位和分布式源成像等。
目前广泛使用的MN解的变体被称为LORETA(低分辨率电磁层析成像)。该解中添加的附加约束是源的拉普拉斯函数最小化，从而导致3D活动的平滑(低分辨率)分布。这一限制已经被生理学上看似合理的假设所证明，即相邻体素的活动是相关的，但这一假设在大脑的某些区域(例如半球间裂)受到了挑战。在这种情况下，LORETA会导致模糊和平滑的解。该研究者和其他研究者提出了对该算法的改进，形成了名为sLORETA、eLORETA、LAURA、VARETA等算法。

在这里，我们使用minimum-norm estimation的方法进行源定位，解决逆问题，这个逆算子已经在示例文件中创建好了，自己创建请看源定位相关教程。因为这个逆问题是不确定的，没有唯一的解决方案，在这里示例通过提供一个正则化参数来进一步约束解决方案，该参数指定了当前估计的相对平滑程度。

1
2
3
4
5
6
7
8
9
10
11
12
# load inverse operator
inverse_operator_file = (
    sample_data_folder / "MEG" / "sample" / "sample_audvis-meg-oct-6-meg-inv.fif"
)
inv_operator = mne.minimum_norm.read_inverse_operator(inverse_operator_file)
# set signal-to-noise ratio (SNR) to compute regularization parameter (λ²)
snr = 3.0
lambda2 = 1.0 / snr**2
# generate the source time course (STC)
stc = mne.minimum_norm.apply_inverse(
    vis_evoked, inv_operator, lambda2=lambda2, method="MNE"
)  # or dSPM, sLORETA, eLORETA

stc就是我们需要的源估计，现在我们要给这个重要的stc画出来，应用到解剖项中，一般是MRI的T1。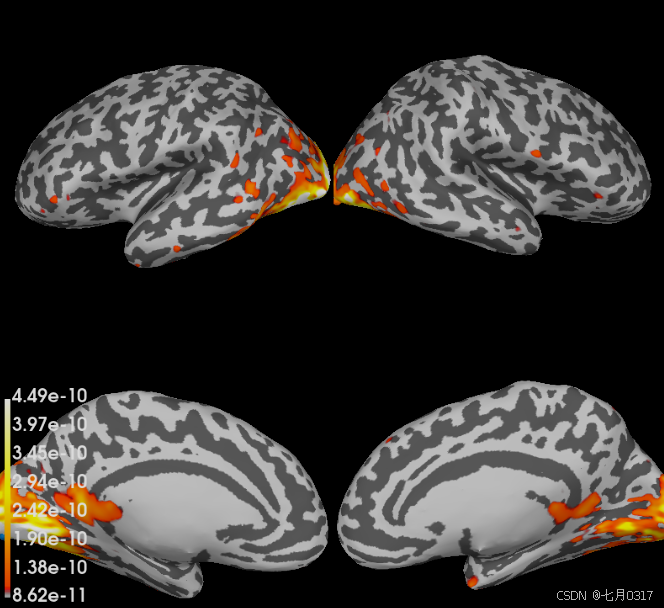
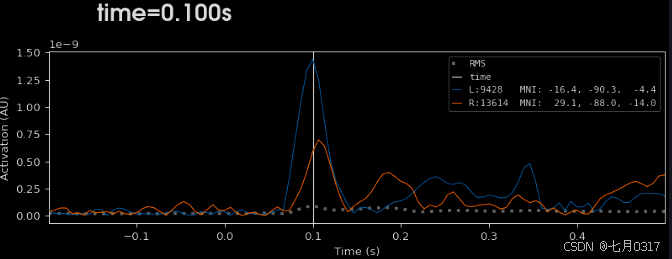
image.png
image.png
入门教程01到此结束。

参考资料
许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

分享文章

在这里🌼留下足迹🐾